Volume Of Cap Of Sphere Calculator

Calculating volume and surface area of sphere play an important role in mathematics and real life as well. Formulas for volume & surface area of sphere can be used to explore many other formulas and mathematical equations. In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere. Volume is the quantification of the three-dimensional space a substance occupies.

The SI unit for volume is the cubic meter, or m3. By convention, the volume of a container is typically its capacity, and how much fluid it is able to hold, rather than the amount of space that the actual container displaces. Volumes of many shapes can be calculated by using well-defined formulas. In some cases, more complicated shapes can be broken down into simpler aggregate shapes, and the sum of their volumes is used to determine total volume. The volumes of other even more complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary. Beyond this, shapes that cannot be described by known equations can be estimated using mathematical methods, such as the finite element method.

Alternatively, if the density of a substance is known, and is uniform, the volume can be calculated using its weight. This calculator computes volumes for some of the most common simple shapes. A spherical segment or a spherical layer is a three-dimensional geometrical object defined by cutting a sphere with a pair of two parallel planes. The top and bottom planes, where intersecting the sphere, create two circles with radii b and a respectively, which serve as top and bottom bases of the segment. The height of the segment is the distance between the bases. The surface of the spherical segment is called spherical zone .

This function calculates the volume and surface area of a spherical cap. A spherical cap or spherical dome is a portion of a sphere cut off by a plane. A spherical cap segment is the solid defined by cutting a sphere with a pair of parallel planes . It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum .

Online calculator to calculate the volume of geometric solids including a capsule, cone, frustum, cube, cylinder, hemisphere, pyramid, rectangular prism, sphere and spherical cap. If you ever wondered what's the volume of the Earth, soccer ball or a helium balloon, our sphere volume calculator is here for you. It can help to calculate the volume of the sphere, given the radius or the circumference.

Also, thanks to this calculator you can determine the spherical cap volume or hemisphere volume. A spherical cap is the region of a sphere which lies above a given plane. If the planepasses through the center of the sphere, the cap is a called a hemisphere, and if the cap is cut by a second plane, the spherical frustum is called a spherical segment. However, Harris and Stocker use the term "spherical segment" as a synonym for what is here called a spherical cap and "zone" for spherical segment. Two online calculators to calculate the volume, surface area and height of a sphrical cup are presented.

The calculators also computes the ratios of the volumes and ares of the cap and the sphere from which the cap is cut. Surface to Volume Ratio is denoted by RAV symbol. A set of points in a space equally distanced from a given point $O$ is a sphere. The point $O$ is called the center of the sphere. The distance from the center of a sphere to any point on the sphere is called the radius of this sphere.

A radius of a sphere must be a positive real number. The segment connecting two points on the sphere and passing through the center is called a diameter of the sphere. All radii of the sphere are congruent to each other. A sphere can be obtained by rotating a semicircle about the diameter. Two spheres of the same radius are congruent.

1 - Enter the radius \( R \) of the sphere from which the spherical cap is cut and the height \( h \) as positive real numbers, with \( R \ge h \) and press "calculate". A spherical segment is the solid defined by cutting a sphere with a pair of parallel planes. It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum. All dome structures described by this calculator are a segment or "cap" of a sphere as defined by the dome's diameter and height. The radius of curvature is the calculated radius of the whole sphere of which the dome is a portion. For any other value for the length of the radius of a sphere, just supply a positive real number and click on the GENERATE WORK button.

They can use these methods in order to determine the surface area and volume of parts of a sphere. Spherical segment is a solid bounded by two parallel planes through a sphere. In terms of spherical zone, spherical segment is a solid bounded by a zone and the planes of a zone's bases. Given a sphere with a diameter of 173' and a sphere cap with a base diameter of 86.5'. I have a scale drawing showing a distance "h" of approximately 11.5'.

I have two excel formulas for calculating "h", the distance from the center of the chord to the center of the arc. Neither formula produces a result that agrees with the scale drawing. One result is 5.9' and one is 7.8'. Any sample formula suggestions would be greatly appreciated. The overall diameter of the structure.

The calculator applies the diameter to the floor, stem wall, and base of the spherical dome. A single diameter input is useful for quick estimates, but when calculating a specific design that may have a different diameter for the stem wall, you should run two separate calculations. A level input measures a slice of the structure. For example, it can calculate the area of a second floor, show headroom around the dome perimeter, or calculate the volume and surface area of a portion of the dome. Spherical cap The spherical cap has a base radius of 8 cm and a height of 5 cm.

Calculate the radius of a sphere of which this spherical cap is cut. To calculate Surface to volume ratio of Spherical Sector given sphere cap radius, you need Height & Radius . With our tool, you need to enter the respective value for Height & Radius and hit the calculate button. You can also select the units for Input and the Output as well.

A spherical cap is the region of a sphere that lies above a given plane. If the plane passes through the center of the sphere, the cap is called a hemisphere. The spherical segment of one base is also called spherical cap and the two bases is also called spherical frustum.

The bases of a spherical segment are the sections made by the parallel planes. The radii of the lower and upper sections are denoted by a and b, respectively. If either a or b is zero, the segment is of one base.

If both a and b are zero, the solid is the whole sphere. Spherical cap Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which the spherical cap was cut.

This concept can be of significance in geometry, to find the volume & surface area of sphere and its parts. Real life problems on volume & surface area of sphere are very common, so this concept can be of great importance of solving problems. Spherical cap Wikipedia.

Volume Cap Of Sphere The sphere is perfectly symmetrical, and has the smallest ratio of surface area to volume of any three-dimensional shape. In other words, for any given volume, the smallest surface area able to completely enclose that volume is a sphere. For this reason the sphere is …, The sphere is perfectly symmetrical, and has the smallest ratio of surface area to volume of any three-dimensional shape. For this reason the sphere is …. If one of the parallel planes is tangent to the sphere, the solid thus formed is a spherical segment of one base. The density of a sphere is defined as the total mass per unit of volume of a spherical object.

Just work with a circle. Draw the radius, say a vertical line. Draw the chord, say a horizontal line so that it intersects the vertical radius. Next, draw the radius to the tip of the chord. What kind of triangle does the chord, the vertical line and the radius to the tip of the chord form? From this you can calculate the distance from the center to the intersection of the vertical radius and the chord.

From that you can get the distance from chord to the top of the arc. The level surface distance is the overall surface distance from the dome apex to the imaginary slice at the specified level. It will correctly follow the dome and even down the stem wall. The stem wall height describes a cylinder's height with the floor diameter and the stem wall height. It connects the floor to the dome base.

Leave the stem wall height set to zero to remove the stem wall. The floor circumference is the distance around the circle-shaped floor, stem wall, and dome base. The height of the stem wall extends vertically from the circular floor to the base of the dome.

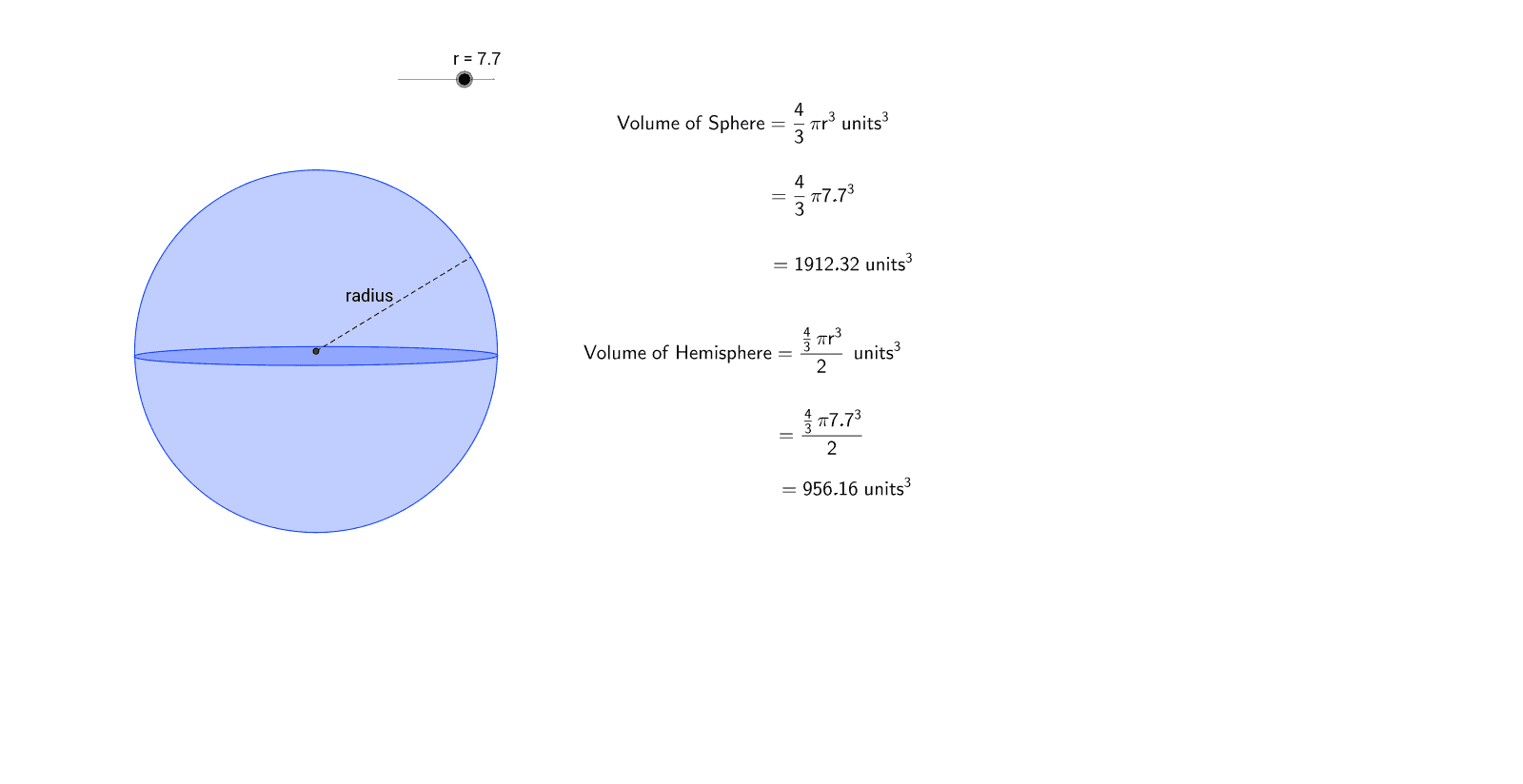
The stem wall height is optional by leaving the height set to zero . Sphere surface area & volume calculator uses radius length of a sphere, and calculates the surface area and volume of the sphere. Sphere calculator is an online Geometry tool requires radius length of a sphere. Using this calculator, we will understand methods of how to find the surface area and volume of the sphere. The total space occupied by a section of the sphere is called the volume of a section of a sphere. A section of a sphere is a portion of a sphere.

The volume of a section of a sphere is expressed in square units. A spherical cap is defined as as a portion of the sphere cut by a plane. Calculations at a spherical cap . A spherical cap ist an evenly cut off part of a sphere. The remaining part is also a spherical cap.

The calotte is the curved part of the cap. Enter radius of the sphere and height of the spherical cap and choose the number of decimal places. The spherical cap volume appears, as well as the radius of the sphere.

They are equal to 287 cu in and 4.2 in for our example. There's the trivial observation that a maximal packing of balls of radius $\alpha/2$ gives a covering of radius $\alpha$. Thus, an upper bound on the maximal number of disjoint balls of radius $\alpha/2$ gives an upper bound on the number of balls of radius $\alpha$ needed to cover. There is the trivial upper bound on the number of spheres of radius $\alpha/2$ by taking the ratio of volumes, but this can be improved using Boroczky's packing estimate.

The MDI Spherical Dome Calculator helps calculate common design elements of a partial sphere set on an optional stem wall. It helps with quick design ideas as well as provides accurate measurements when finalizing structural elements. Outputs include circumference, surface area, volume, and distances along and around the building's various details. Many sports that are played with the help of the ball require studying the sphere, as well as its properties.

For example, in football, the surface area and volume of a ball is of extreme importance. Different volumes and surface areas of a ball can affect to speed of the kick, trajectory of the ball and its swing in the air. Apart from football, the surface area and volume of a sphere is important in many other sports as well.

Tennis, handball, baseball, golf, basketball all these sports are revolving around the spherical balls. Any cross section of a sphere by a plane is a circle. The circle obtained as a cross section of the sphere and plane through the center of the sphere is called a great circle. Any plane that passes through the center $O$ of a sphere divides it into two congruent parts well-known as hemispheres. As we learned in the previous section, the volume of the spherical segment is (1/6)πh(3R12 + 3R22 + h2).

Thus, we follow the steps shown below to find the volume of the spherical segment. As we learned in the previous section, the volume of the spherical cap is (1/3)πh2(3R - h) or (1/6)πh(3a2 + h2). Thus, we follow the steps shown below to find the volume of the spherical cap. In this section, we will discuss the volume of a section of a sphere along with solved examples. Let us start with the pre-required knowledge to understand the topic, volume of a section of a sphere. The volume of a three-dimensional object is defined as the space occupied by the object in a three-dimensional space.

Calculates the volume and surface area of a partial sphere given the radius and height. To calculate the volume of the full sphere, use the basic calculator. Enter the radius 4.2 in. Appear in the formula.

Do Air And Water Signs Mix

There are many different factors that play into the astrological compatibility between two people, but if we want to simplify things, looking at elements can help us make some generalized guesses. Certain elements complement each other to form a good union, while others can clash and make relationships a little extra challenging. Firstly, if someone's zodiac sign shares an element with yours, you're more likely to be compatible with them.

This is because you instinctively understand each other's ways of thinking and motivations, so there's an easy vibe between you. You'll also usually pair well with the element of the sign that's directly across from yours on the zodiac wheel — so that pairs fire signs with air signs, and earth signs with water signs. The reason for this is that there's a naturally give and take between these opposing energies. You work well in symbiosis and bring each other something others can't. Conversely, fire and air signs might struggle more with water and earth signs, and vice versa. This is because their ways of dealing with things could clash, and it's harder to find common ground.

What is also apparent from that view is that earth and fire are centred primarily in the outer world; while air and water are centred much more in themselves and in human beings, relationships. The engagement of earth signs with money, with job of work, with politics and status are all worldly matters. There also appears to be a problem with Mercury and Venus, both being rulers of earth and of air signs. Being in earth, Mercury seems to create a Virgo gloss over things and with an essentially masculine vibe. Venus in air seems to give a basically Libra feel and also a feminine gloss. Those who belong to the air sign group have outstanding communication skills.

Due to this air signs are compatible with fellow air signs, fire signs as well as water signs. But they don't share the same bonding with the earth signs. The connection between two individuals under the same air signs could seem impractical but they consider each other intellectually stimulating.

The combination of an earth sign and air sign can only work if both of them are ready to stay together as a team. If the partner with the air sign starts criticising their partner a lot, they might be let down. If you take the time to analyze how your ruling element reacts to conflict, you can figure out how to improve the way you deal with it, which is always a good thing. Keep in mind that air signs tend to get caught up in thinking about things too much, while fire signs may run toward conflict too aggressively at times and jump to quick conclusions. Earth signs, on the other hand, can be a little stubborn and overly-pragmatic, while water signs can get too worked up in their emotions and take things personally. The same elements usually have an easier time of it simply because there's an intrinsic understanding of each other.

Air sign family members often share a quirky sense of humour, upbeat temperament and curiosity. The environment between two grounded earth signs is also relatively effortless. A Capricorn parent and Taurus child will revel in each other's company without the need for too much verbal communication, and there's likely to be less squabbling among earth siblings. When it comes to water signs or fire signs though emotions tend to run high.

Do Water And Air Signs Get On While there's a tacit understanding between them and the wonderful ability to intuit each other's needs water signs are prone to sulky stand-offs. A Scorpio might become annoyed by Pisces' heightened sensitivity; Pisces may find Cancer to be overbearing while Cancer will battle with a Scorpio's intensity and lack of communication. On a good day life is one big adventure for passionate, enthusiastic and big-hearted fire signs. However, when an opinionated Sagittarius, straightforward Aries or feisty Leo disagree there's likely to be pyrotechnics, and not the New Year's Eve variety. As long as there is compromise and an effort to avoid bad behavioural patterns the pros usually outweigh the cons. All the zodiac signs under the element of earth are highly compatible with fellow earth signs and tend to appreciate each other's need for stability and find comfort in each other.

This combination is very soothing and promotes inner peace. The stable and dependable traits of the earth sign balance the sensitive and emotional traits of the water signs. The traits of earth signs are difficult to deal with for the enthusiastic signs under the fire element. Therefore, these two are never a suitable match for each other. Leo, Aries, and Sagittarius are the fire signs who carry their passion and drive with them everywhere they go.

Meanwhile, air signs Gemini, Aquarius, and Libra propel the world forward using their intellect and mental prowess. Water signs Scorpio, Pisces, and Cancer keep people in touch with their emotions by feeling all of their feelings, all the time. And the earth signs Virgo, Capricorn, and Taurus remind us all to stay grounded and embrace practicality, even when it's difficult. We all love finding out more about our zodiac signs, but there is so much more to astrology than just reading your horoscope for the day.

We are great together but that doesn't mean I would have the same experience with surgery air sign. There is a lot more to astrology than just sun signs and elements. On the surface we make no sense but when you dig down deep you begin to understand. Every once in awhile you get your exceptions but best bet for a water sign is usually other water signs or an earth sign. Air component zodiac signs aren't truly viable with earth component represented signs, for example, Taurus, Virgo and Capricorn. The air works up residue when the two components connect, making earth agitated.

Earth component sign view Aquarius' air signs as ridiculous and even whimsical since they don't follow show and aren't grounded like earth signs. However these aren't one of the elements that question is Aquarius a water sign or an air sign. Even our tides are linked to the full moon and the new moon, reaching maximum intensity when the moon is the most waxed or waned. If the fire signs embody a solar or Martian energy, if the air signs are amorphous and mercurial, and if the earth signs are fertile and Venusian, the water signs are deep and lunar. A fire sign and water sign are not easy signs to get along well and can bring out the worst in each other. This is because water signs are sensitive and emotional beings.

Whereas Fire signs are straightforward and will say what they feel. Water likes to flow gently on its own time and rhythm, while Fire ignites and burns bright with a glow. As in nature, water can extinguish fire, so is true in life. Too much fire can dehydrate delicate sensitivities of watery signs and overwhelming emotions may douse the enthusiasm and drain the energy of Fire signs.

Every fire sign is independent and on a certain level, they need the freedom to express themselves to be happy. Water signs love deep and are mostly intuitive, maybe psychic to read between the lines and get easily affected by underlying vibes. Water signs tend to recall what you said to them in the past and also to suffer over harsh words.

The aggression of Aries, the ego of Leo and bluntness of Sagittarius is brought to the surface; often there are ego clashes leaving fire signs snapping angrily and water signs sulking. When they are together, neither of them adopts a logical position, and keep building harmful emotions up inside, until exploding at some point. Fire and Water drain each other's energy and bring out the worst in each other. There is a divine plan in place; the sacred contract ensures each soul mate needs to perfect their soul and find ways to control the worst that surface in you.

"Astrologers often say that the remedy for any sign's neurosis is the enlightened qualities of the opposite sign," McCarthy says. Air and water are also opposite elements – air signs tend to be logical and verbal whereas water is intuitive and emotive – so there's usually a lot of effort involved. A Scorpio parent will at times be intolerant of a Gemini child's chatter.

Similarly, an Aquarius won't relate to the sentimental nature of a Cancer. However, these family members can have a beneficial and balancing influence on each other. Air signs can teach water to experience life without being bogged down by their emotions. Water, in turn, can encourage air to be emotionally expressive rather than objectify their feelings.

So, what are the major strengths and weaknesses of each element? Earth signs are grounded and logical, but can be stuck in their ways or overly stubborn about straying from the beaten path. Fire signs are inspiring and exciting to be around, but can lack tact when it comes to forcing ideas upon people or controlling their impulses. Water signs are deeply sensitive and spiritual, and help others get in touch with their emotions — but can too easily get sucked into other people's feelings and dramas if they're not careful. And air signs remind people to be free-thinking and quick-moving, but can sometimes be detached, flighty, and hard to rely on.

Thus the positive signs tend to show outlets into the world from the individual , while the negative signs and houses show where movement occurs inwards fromthe world into the individual . Ah,Pisces, our cosmic mermaids, able to walk through our earthly realm while immersing themselves in the depths of others' emotions. They sense when you're lying about your weekend plans or anxious about a new job. One of the four mutable signs of the zodiac, Pisces can shapeshift to match the energy of any room.

The intuitive water signs will find themselvesempathizingwith the thoughts and feelings of their crew. If you ask the slippery sign which TV show they'd like to watch, adaptable Pisces is eager to go along with the choice that brings you joy. But when it comes to their alone time, Pisceans are particular about how they unwind and escape . Water tends to share a pleasant relationship with fellow earth signs, there is a great mix of energies that will promote a healthy and balanced relationship.

Water likes to flow gently on its own time and rhythm, while air wants to make movements and stir things up. The individuals under these two signs may end up disliking each other. Two individuals under the same water signs will be sensitive to each other's needs, but it will be very difficult for them to deal with emotional turmoil of each other. Pisces is a water sign, and therefore compatible with other water signs, Cancer and Scorpio. With the water signs, the element of romance is very strong and this couple will intuitively understand each other. They base relationships on looking after each other and developing a really strong emotional connection.

They like to share how they feel and create memories together. Scorpio is a water sign, and therefore compatible with other water signs, Cancer and Pisces. Cancer is a water sign, and therefore compatible with other water signs, Scorpio and Pisces.

Understanding the element and modality of the zodiac signs is just the beginning. To determine whether you've met a love match, it's essential to consider that the signs of each planet, the astrological houses, and the aspects all have a say. If a couple is earnest about understanding their relationship, they should seek a professional astrologer for a relationship synastry consultation. When it comes to modality combinations, one isn't necessarily easier than the other – there are pros and cons for each.

Being so focused and ambitious cardinal signs may find mutable signs are too easy-going and lacking in direction. Mutable signs on the other hand will view cardinal signs as being too are bossy and, at times, full of bravado. Cardinal and fixed signs are likely to lock horns over change.

However, once cardinal back offs and makes fixed feel needed their vision and stamina will complement each other perfectly. It is also important to observe the amount of each element in the chart as that gives clues to the mentality and life pattern. In a fundamentally water type of chart the aspects to the water planets are certainly the most important and have precedence over all other aspects.

In a 'fire chart', all aspects to the fire planets take precedence over all other aspects. Likewise, in a predominantly air chart only the air signs and air planets need to be considered in delineating huge areas of the mentality and life pattern. Thus from considerations of this kind, a lot of sense can be made of a chart just through considering the elemental bias the chart seems to contain. For example, a chart with a water sign rising and prominent water planets can be considered a 'water chart'.

Now, when it comes to what the other elements think of air signs, it's kind of a mixed bag. An emotional water sign might find the air signs to be a bit cold, while earth signs will be too stale and stable for air signs. But fire signs—ah, fire signs—they're all about the air signs. The feeling's mutual because "air feeds fire," Montúfar says. Air can be gentle and we all need air to breathe, but don't jump to hasty conclusions.

Statistically, air kills more people in one way or another (covid-19 has made us realize this truth). Those who belong to the air sign group are quick, curious, charming and maybe flirtatious. Earth signs are stable and sensual, and they rule the physical world. Earth sign—Taurus look for financial stability, Virgo go for methodical planning and Capricorn are committed workers. Air sign may find practical Earth sign people rigid and so, Air and Earth sign may criticize each other for their respective choices.

The traits of earth signs are difficult to deal with for the enthusiastic Air sign; these two are not a suitable match for each other. However, blocking out your soul contracts with even the most annoying people that don't serve you. Understanding simple practices to just disengage and hold onto your sanity is better. There are four elements in astrology, namely—fire, earth, air and water. The zodiac signs belonging to these groups tend to take on the characteristics of the element which are largely responsible for an individual's temperament and its relationship with others. The laws of chemistry define the actions of fire, water, earth, and air in the real world, likewise, the zodiac signs behave in a similar manner, which is why some signs bring out the worst in others.

The elements combine astrologically the same way as they do in nature. The same element form the most beautiful mathematical trine/ 180° angles to each other and the worst compatible are those forming square/90 °. In the realms of nature, water and earth mutually benefit each other and so the relationship between these family members is usually strong and effortless. Earth signs have the patience to cope with the moods and complexities of water. Water, in turn, provides emotional support and a comfortable environment for earth signs to air their feelings.

However, a Taurus, for example, may become irritated by a Scorpio's sensitivity while a Pisces will see a Virgo as being too uptight, but the cons are minimal. Water signs compel earth to be more perceptive and compassionate while earth provides water with stability and calm. Between Cancer's moods and Leo's ego, you're a camera crew away from being a reality show—the kind that makes you want to change the channel, only you can't leave the crash scene. Your signs are both needy and bossy, but in different ways. Cancer is insecure and possessive, and this sign's sensitive Water element can quench Fire-sign Leo's excitement.