Volume Of Cap Of Sphere Calculator

Calculating volume and surface area of sphere play an important role in mathematics and real life as well. Formulas for volume & surface area of sphere can be used to explore many other formulas and mathematical equations. In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere. Volume is the quantification of the three-dimensional space a substance occupies.

The SI unit for volume is the cubic meter, or m3. By convention, the volume of a container is typically its capacity, and how much fluid it is able to hold, rather than the amount of space that the actual container displaces. Volumes of many shapes can be calculated by using well-defined formulas. In some cases, more complicated shapes can be broken down into simpler aggregate shapes, and the sum of their volumes is used to determine total volume. The volumes of other even more complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary. Beyond this, shapes that cannot be described by known equations can be estimated using mathematical methods, such as the finite element method.

Alternatively, if the density of a substance is known, and is uniform, the volume can be calculated using its weight. This calculator computes volumes for some of the most common simple shapes. A spherical segment or a spherical layer is a three-dimensional geometrical object defined by cutting a sphere with a pair of two parallel planes. The top and bottom planes, where intersecting the sphere, create two circles with radii b and a respectively, which serve as top and bottom bases of the segment. The height of the segment is the distance between the bases. The surface of the spherical segment is called spherical zone .

This function calculates the volume and surface area of a spherical cap. A spherical cap or spherical dome is a portion of a sphere cut off by a plane. A spherical cap segment is the solid defined by cutting a sphere with a pair of parallel planes . It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum .

Online calculator to calculate the volume of geometric solids including a capsule, cone, frustum, cube, cylinder, hemisphere, pyramid, rectangular prism, sphere and spherical cap. If you ever wondered what's the volume of the Earth, soccer ball or a helium balloon, our sphere volume calculator is here for you. It can help to calculate the volume of the sphere, given the radius or the circumference.

Also, thanks to this calculator you can determine the spherical cap volume or hemisphere volume. A spherical cap is the region of a sphere which lies above a given plane. If the planepasses through the center of the sphere, the cap is a called a hemisphere, and if the cap is cut by a second plane, the spherical frustum is called a spherical segment. However, Harris and Stocker use the term "spherical segment" as a synonym for what is here called a spherical cap and "zone" for spherical segment. Two online calculators to calculate the volume, surface area and height of a sphrical cup are presented.

The calculators also computes the ratios of the volumes and ares of the cap and the sphere from which the cap is cut. Surface to Volume Ratio is denoted by RAV symbol. A set of points in a space equally distanced from a given point $O$ is a sphere. The point $O$ is called the center of the sphere. The distance from the center of a sphere to any point on the sphere is called the radius of this sphere.

A radius of a sphere must be a positive real number. The segment connecting two points on the sphere and passing through the center is called a diameter of the sphere. All radii of the sphere are congruent to each other. A sphere can be obtained by rotating a semicircle about the diameter. Two spheres of the same radius are congruent.

1 - Enter the radius \( R \) of the sphere from which the spherical cap is cut and the height \( h \) as positive real numbers, with \( R \ge h \) and press "calculate". A spherical segment is the solid defined by cutting a sphere with a pair of parallel planes. It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum. All dome structures described by this calculator are a segment or "cap" of a sphere as defined by the dome's diameter and height. The radius of curvature is the calculated radius of the whole sphere of which the dome is a portion. For any other value for the length of the radius of a sphere, just supply a positive real number and click on the GENERATE WORK button.

They can use these methods in order to determine the surface area and volume of parts of a sphere. Spherical segment is a solid bounded by two parallel planes through a sphere. In terms of spherical zone, spherical segment is a solid bounded by a zone and the planes of a zone's bases. Given a sphere with a diameter of 173' and a sphere cap with a base diameter of 86.5'. I have a scale drawing showing a distance "h" of approximately 11.5'.

I have two excel formulas for calculating "h", the distance from the center of the chord to the center of the arc. Neither formula produces a result that agrees with the scale drawing. One result is 5.9' and one is 7.8'. Any sample formula suggestions would be greatly appreciated. The overall diameter of the structure.

The calculator applies the diameter to the floor, stem wall, and base of the spherical dome. A single diameter input is useful for quick estimates, but when calculating a specific design that may have a different diameter for the stem wall, you should run two separate calculations. A level input measures a slice of the structure. For example, it can calculate the area of a second floor, show headroom around the dome perimeter, or calculate the volume and surface area of a portion of the dome. Spherical cap The spherical cap has a base radius of 8 cm and a height of 5 cm.

Calculate the radius of a sphere of which this spherical cap is cut. To calculate Surface to volume ratio of Spherical Sector given sphere cap radius, you need Height & Radius . With our tool, you need to enter the respective value for Height & Radius and hit the calculate button. You can also select the units for Input and the Output as well.

A spherical cap is the region of a sphere that lies above a given plane. If the plane passes through the center of the sphere, the cap is called a hemisphere. The spherical segment of one base is also called spherical cap and the two bases is also called spherical frustum.

The bases of a spherical segment are the sections made by the parallel planes. The radii of the lower and upper sections are denoted by a and b, respectively. If either a or b is zero, the segment is of one base.

If both a and b are zero, the solid is the whole sphere. Spherical cap Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which the spherical cap was cut.

This concept can be of significance in geometry, to find the volume & surface area of sphere and its parts. Real life problems on volume & surface area of sphere are very common, so this concept can be of great importance of solving problems. Spherical cap Wikipedia.

Volume Cap Of Sphere The sphere is perfectly symmetrical, and has the smallest ratio of surface area to volume of any three-dimensional shape. In other words, for any given volume, the smallest surface area able to completely enclose that volume is a sphere. For this reason the sphere is …, The sphere is perfectly symmetrical, and has the smallest ratio of surface area to volume of any three-dimensional shape. For this reason the sphere is …. If one of the parallel planes is tangent to the sphere, the solid thus formed is a spherical segment of one base. The density of a sphere is defined as the total mass per unit of volume of a spherical object.

Just work with a circle. Draw the radius, say a vertical line. Draw the chord, say a horizontal line so that it intersects the vertical radius. Next, draw the radius to the tip of the chord. What kind of triangle does the chord, the vertical line and the radius to the tip of the chord form? From this you can calculate the distance from the center to the intersection of the vertical radius and the chord.

From that you can get the distance from chord to the top of the arc. The level surface distance is the overall surface distance from the dome apex to the imaginary slice at the specified level. It will correctly follow the dome and even down the stem wall. The stem wall height describes a cylinder's height with the floor diameter and the stem wall height. It connects the floor to the dome base.

Leave the stem wall height set to zero to remove the stem wall. The floor circumference is the distance around the circle-shaped floor, stem wall, and dome base. The height of the stem wall extends vertically from the circular floor to the base of the dome.

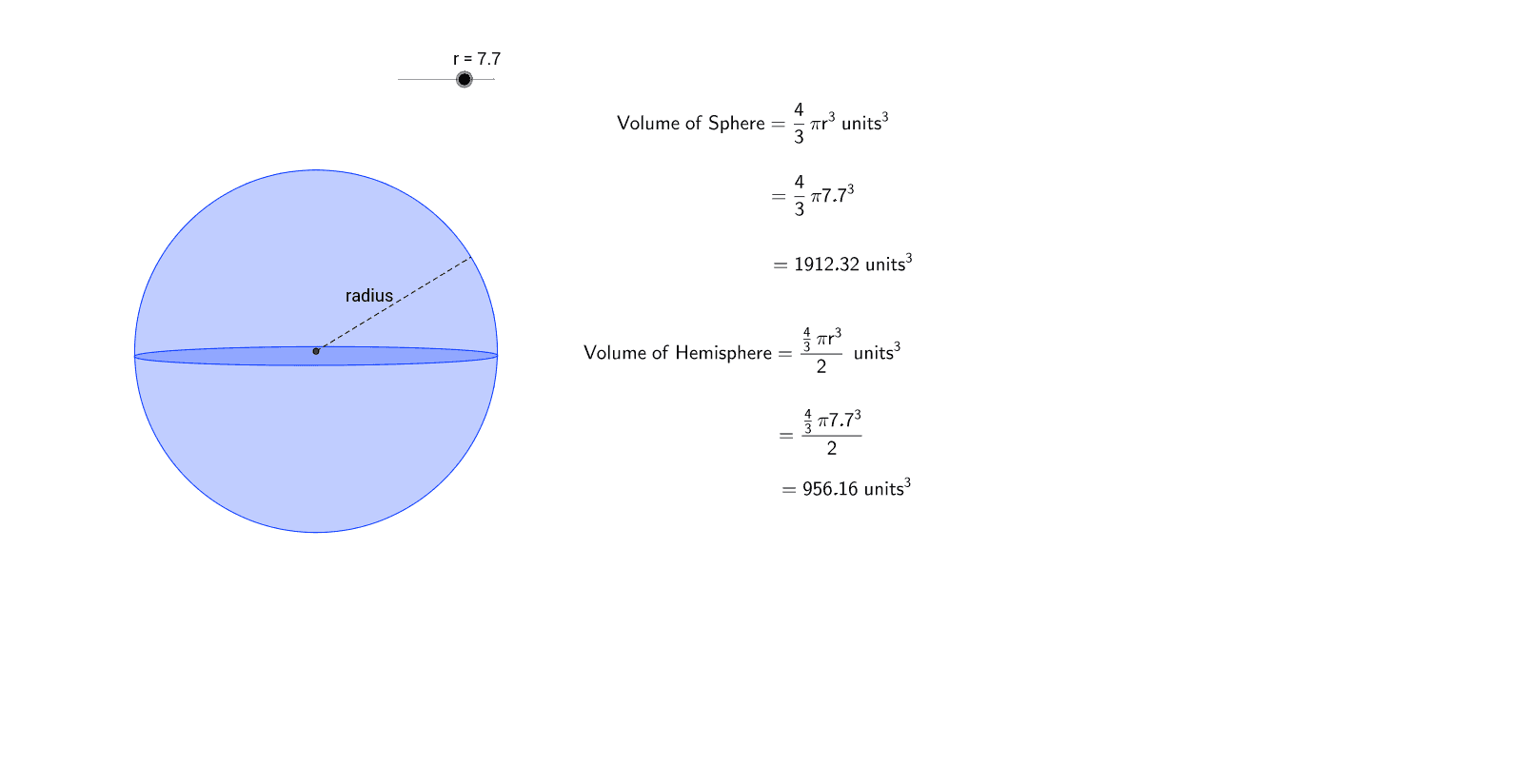
The stem wall height is optional by leaving the height set to zero . Sphere surface area & volume calculator uses radius length of a sphere, and calculates the surface area and volume of the sphere. Sphere calculator is an online Geometry tool requires radius length of a sphere. Using this calculator, we will understand methods of how to find the surface area and volume of the sphere. The total space occupied by a section of the sphere is called the volume of a section of a sphere. A section of a sphere is a portion of a sphere.

The volume of a section of a sphere is expressed in square units. A spherical cap is defined as as a portion of the sphere cut by a plane. Calculations at a spherical cap . A spherical cap ist an evenly cut off part of a sphere. The remaining part is also a spherical cap.

The calotte is the curved part of the cap. Enter radius of the sphere and height of the spherical cap and choose the number of decimal places. The spherical cap volume appears, as well as the radius of the sphere.

They are equal to 287 cu in and 4.2 in for our example. There's the trivial observation that a maximal packing of balls of radius $\alpha/2$ gives a covering of radius $\alpha$. Thus, an upper bound on the maximal number of disjoint balls of radius $\alpha/2$ gives an upper bound on the number of balls of radius $\alpha$ needed to cover. There is the trivial upper bound on the number of spheres of radius $\alpha/2$ by taking the ratio of volumes, but this can be improved using Boroczky's packing estimate.

The MDI Spherical Dome Calculator helps calculate common design elements of a partial sphere set on an optional stem wall. It helps with quick design ideas as well as provides accurate measurements when finalizing structural elements. Outputs include circumference, surface area, volume, and distances along and around the building's various details. Many sports that are played with the help of the ball require studying the sphere, as well as its properties.

For example, in football, the surface area and volume of a ball is of extreme importance. Different volumes and surface areas of a ball can affect to speed of the kick, trajectory of the ball and its swing in the air. Apart from football, the surface area and volume of a sphere is important in many other sports as well.

Tennis, handball, baseball, golf, basketball all these sports are revolving around the spherical balls. Any cross section of a sphere by a plane is a circle. The circle obtained as a cross section of the sphere and plane through the center of the sphere is called a great circle. Any plane that passes through the center $O$ of a sphere divides it into two congruent parts well-known as hemispheres. As we learned in the previous section, the volume of the spherical segment is (1/6)πh(3R12 + 3R22 + h2).

Thus, we follow the steps shown below to find the volume of the spherical segment. As we learned in the previous section, the volume of the spherical cap is (1/3)πh2(3R - h) or (1/6)πh(3a2 + h2). Thus, we follow the steps shown below to find the volume of the spherical cap. In this section, we will discuss the volume of a section of a sphere along with solved examples. Let us start with the pre-required knowledge to understand the topic, volume of a section of a sphere. The volume of a three-dimensional object is defined as the space occupied by the object in a three-dimensional space.

Calculates the volume and surface area of a partial sphere given the radius and height. To calculate the volume of the full sphere, use the basic calculator. Enter the radius 4.2 in. Appear in the formula.